[백준] 1715번 - 카드 정렬하기 (Gold 4)

업데이트: August 12, 2022

문제 링크

문제 설명

매우 많은 수의 정렬된 숫자 카드 묶음이 있다.
카드 묶음은 한번에 두 묶음씩만 합칠 수 있으며, A장으로 이루어진 카드 묶음과 B장으로 이루어진 카드 묶음을 합치는데는 A+B번의 비교가 필요하다.
모든 카드 묶음을 합치는데 필요한 최소 비교 횟수를 구하시오.

정답 코드 및 설명

가장 작은 두 개의 카드 묶음을 합치는 과정을 반복하는 것이 최소로 비교하는 방법이다.
이는 우선순위 큐를 활용하면 쉽게 구현이 가능하다.
그리디한 방법으로 구한 횟수가 최소임이 직관적으로는 당연하지만, 사실 증명이 필요하다.
증명이 궁금한 분들을 위해 맨 아래에 증명을 따로 적어두었다.

사실 이 문제는 Huffman Coding과 본질적으로 같은 문제이다.
Huffman Coding은 문자의 빈도수를 이용해서 파일을 압축하는 과정인데, 문자의 빈도수가 이 문제의 각 카드 묶음 크기에 대응된다고 볼 수 있다. Huffman Coding에 대해 더 자세히 알고 싶다면, 위키피디아를 참고하자.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;

public class BOJ1715 {
    int n;
    PriorityQueue<Integer> cards;

    void input() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        cards = new PriorityQueue<>();
        for (int i = 0; i < n; i++)
            cards.add(Integer.parseInt(br.readLine()));
    }

    long count() {
        long count = 0;
        while (cards.size() > 1) {
            int first = cards.poll();
            int second = cards.poll();
            cards.add(first + second);
            count += first + second;
        }
        return count;
    }

    void solution() throws IOException {
        input();
        System.out.println(count());
    }

    public static void main(String[] args) throws IOException {
        new BOJ1715().solution();
    }
}

증명

증명은 사이트를 참고하였다.

트리 표현

카드 묶음을 합치는 과정은 트리로 표현이 가능하다.
문제 본문에 있는 예시인 10장, 20장, 40장의 세 개의 묶음이 있는 경우를 생각하자.
먼저, 10장과 20장을 먼저 합치고 40장을 나중에 합친 경우이다. 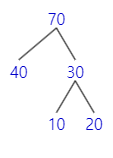그림 1 : 10장과 20장을 먼저 합친 경우

두번째로, 10장, 40장을 먼저 합치고 20장을 나중에 합친 경우이다. 그림 2 : 10장과 40장을 먼저 합친 경우

보조 정리

최적의 묶는 방식을 나타내는 트리의 가장 깊은 리프 노드 두 개는 가장 작은 크기의 묶음 두 개에 대응된다.

묶음을 합치는 과정을 트리로 표현했을 때 다음과 같은 사실들을 알 수 있다.

리프 노드의 수는 처음 묶음의 개수와 같다.
처음 주어진 카드 묶음에 대응하는 리프 노드가 하나씩 있다.
부모 노드의 값은 자식 노드의 값들의 합이다.
전체 비교 횟수는 리프 노드가 아닌 모든 노드의 값의 합이다.
전체 비교 횟수는 각 리프 노드의 값과 깊이를 곱한 값의 합이다.

5번 사실에 의해, 최적의 묶는 방식을 나타내는 트리는 항상 가장 작은 크기의 묶음 두 개가 깊이가 최대인 리프 노드에 대응됨을 알 수 있다. 그렇지 않다면, 깊이가 최대인 리프 노드의 값과 묶음의 크기 중 가장 작은 값을 교환하면 더 효과적인 묶는 방식이 나오기 때문이다.

본 증명

이제 크기가 가장 작은 묶음 두개를 묶는 과정을 반복하는 것이 최적임을 증명하자.
수학적 귀납법을 사용하여 증명할 수 있다.

귀납 가정

묶음의 개수가 N개일 때 최적의 묶는 방식은 가장 작은 두 개의 묶음을 합치는 과정을 반복하는 것이다.

N = 2인 경우 귀납 가정은 참이다.
- N = 2인 경우 묶는 방식은 유일하기 때문이다.
N = K인 경우 귀납 가정이 참이라고 가정하자.
N = K + 1인 경우
- 보조 정리에 의해, 최적화된 묶는 방식에서 가장 먼저 묶는 두 개의 묶음은 크기가 가장 작은 둘이다.
- 두 개를 묶고 나면 K개의 묶음이 남으므로 귀납 가정에 의해 가장 작은 두 개의 묶음을 합치는 과정을 반복하는 것이 최적이다.
- 둘을 합치면, N = K + 1일 때도 귀납 가정이 참이다!

Twitter Facebook LinkedIn

길사