[백준] 25308번 - 방사형 그래프 (Gold 4)

문제 링크

백준 25308번 - 방사형 그래프 (Gold 4)

문제 설명

8개의 능력치 $(a_1, a_2, \cdots, a_8)$을 방사형 그래프로 나타내려고 한다.
방사형 그래프는 k번째 능력치를 원점을 기준으로 반지름 $a_k$, 편각 45k도인 점에 대응시키고, 8개의 점을 k = 1부터 시작해서 k = 8까지 순서대로 이은 후 마지막에 k = 8과 k = 1인 점을 이어 팔각형을 만든 것이다.

능력치가 주어져 있을 때, 능력치의 순서를 적절히 바꿔서 방사형 그래프가 볼록 다각형이 되도록 할 수 있는 경우의 수를 구하시오.

정답 코드 및 설명

시작점을 하나로 고정하고, 나머지 7개의 점만을 배치하는 경우의 수를 구한 후 8을 곱하면 된다.
고려해야 할 모든 경우의 수가 7! = 5,040으로 매우 작으므로, 백트래킹을 통해 풀 수 있다.

이제 각 경우의 수에 대해 어떤 조건을 만족해야 볼록 다각형이 되는지를 살펴보자.
$a_k$에 해당하는 점이 $a_{k - 1}$에 해당하는 점과 $a_{k + 1}$에 해당하는 점을 잇는 선분을 기준으로 원점의 반대편에 있으면 점 $a_{k - 1}$ - 점 $a_k$ - 점 $a_{k + 1}$로 이루어진 각은 180도보다 작다.
단, $a_{0} = a_{8}, a_{9} = a_{1}$로 생각한다.

이 상황을 그림으로 나타내보자.

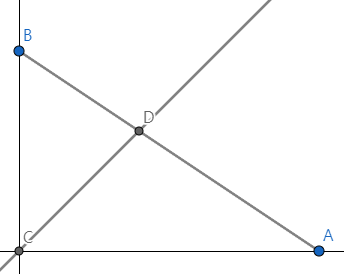그림 1 : C는 원점, A는 $a_{k -1}$에 해당하는 점, B는 $a_{k + 1}$에 해당하는 점, D는 선분 AB 위의 점 중 편각이 45도인 점

선분 CD의 길이보다 $a_k$가 크다면 볼록 다각형이 되는 것이다.
각의 이등분선 정리에 의해, $\overline{BD} : \overline{CD} = \overline{BC} : \overline{CA} = a_{k + 1} : a_{k - 1}$이고 점 B의 좌표는 $(0, a_{k + 1})$, 점 A의 좌표는 $(a_{k - 1}, 0)$이다.
따라서 점 D의 좌표는 $(a_{k - 1} a_{k + 1}, a_{k - 1} a_{k + 1}) / (a_{k - 1} + a_{k + 1})$이 되고 $\overline {CD} = \sqrt{2} \times a_{k - 1}a_{k + 1} / (a_{k - 1} + a_{k + 1})$이다.
결론적으로, 모든 $k = 1, \cdots , 8$에 대해 $a_{k} > \sqrt{2} \times a_{k - 1}a_{k + 1} / (a_{k - 1} + a_{k + 1})$를 만족하는지를 확인하면 방사형 그래프가 볼록다각형인지를 확인할 수 있다.

이를 코드로 구현하면 아래와 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class BOJ25308 {
    final int TYPES = 8;
    int[] status = new int[TYPES];
    int[] seq = new int[TYPES];
    boolean[] check = new boolean[TYPES];
    int count = 0;

    void input() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 0; i < TYPES; i++) {
            status[i] = Integer.parseInt(st.nextToken());
        }
        seq[0] = status[0];
        check[0] = true;
    }

    void backtracking(int depth) {
        if (depth == TYPES) {
            if (isConvex(0) && isConvex(1)) count++;
            return;
        }
        for (int i = 1; i < 8; i++) {
            if (check[i]) continue;
            seq[depth] = status[i];
            if (depth < 2 || isConvex(depth)) {
                check[i] = true;
                backtracking(depth + 1);
                check[i] = false;
            }
        }
    }

    boolean isConvex(int curr) {
        int before = (curr + TYPES - 2) % TYPES;
        int middle = (curr + TYPES - 1) % TYPES;
        int next = curr % TYPES;
        double line = Math.sqrt(2) * seq[before] * seq[next] / (seq[before] + seq[next]);
        return seq[middle] > line;
    }

    void solution() throws IOException {
        input();
        backtracking(1);
        System.out.println(count * TYPES);
    }

    public static void main(String[] args) throws IOException {
        new BOJ25308().solution();
    }
}